Кинематический анализ планетарной коробки передач

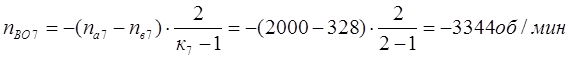
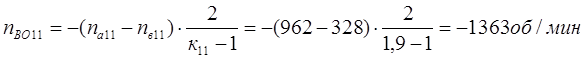
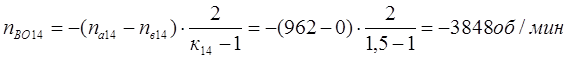
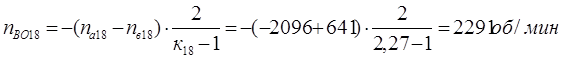
Третья передача. Она обеспечивается включением тормоза Т3. Здесь под нагрузкой работают планетарные ряды 7, 11 и 14.

Перепишем уравнения кинематики ТДМ для указанных планетарных рядов:

При включении тормоза Т3 на данной передаче (см. рис. 3) nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18=0; nв14= nс11= nс18.

Решая уравнения кинематики с учетом уравнений связи, определим передаточное число ПКП:

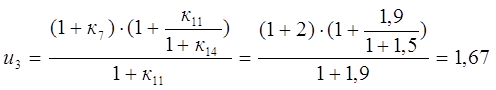
Из схемы ПКП следует, что

Из уравнения кинематики для планетарного ряда 11,14 и 18 с учетом уравнений связи определим

Из уравнения кинематики для планетарного ряда 11 и 7 с учетом уравнений связи определим

Из уравнения кинематики для планетарного ряда 18 с учетом уравнений связи определим

Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:

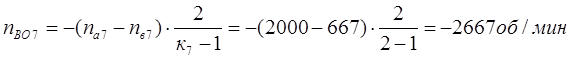
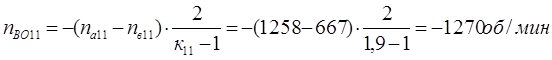
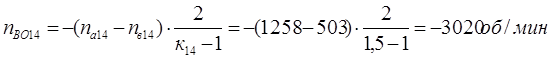
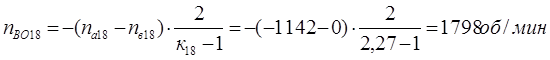
Четвертая передача. Она обеспечивается включением тормоза Т4. Здесь под нагрузкой работают планетарные ряды 7, 11, 14 и 18.

При включении тормоза Т4 на данной передаче (см. рис. 3) nв7= nв11; nа7=nвщ; nа11= nа14=nвм; nс14= nс7= nв18; nв14= nс11= nс18; nа18=0.

Решая уравнения кинематики с учетом уравнений связи, определим передаточное число ПКП:

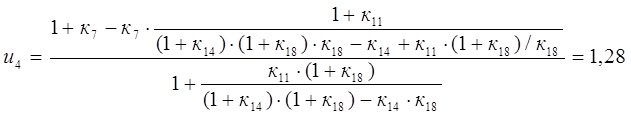
Из схемы ПКП следует, что

Из уравнения кинематики для планетарного ряда 7,14 и 18 с учетом уравнений связи определим

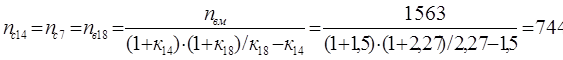
Из уравнения кинематики для планетарного ряда 11,14 и 18 с учетом уравнений связи определим

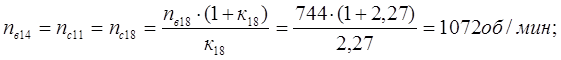
Из уравнения кинематики для планетарного ряда 11 с учетом уравнений связи определим

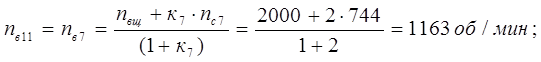
Определим относительные частоты вращения всех сателлитов ПКП при включенной первой передаче. Для этого используем выражение [1,2.11]. В результате получим:

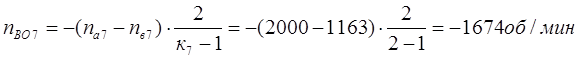
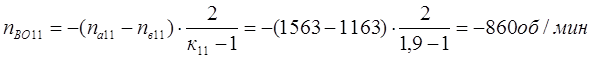
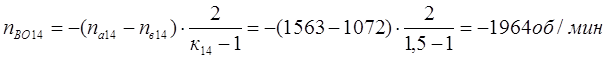
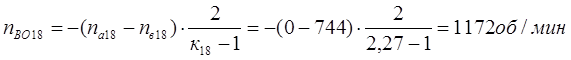
Частоты вращения всех центральных звеньев ПКП и

относительные частоты вращения сателлитов, об/мин

Таблица 5

Еще о транспорте:

Охрана труда
В России существует государственная система стандартов безопасности труда, устанавливающая общие требования безопасности работ (ГОСТ 12.3.017 - 85), которые проводятся на автотранспортных предприятиях, станциях ТО и специализированных центрах при всех видах технического обслуживания и текущего ремо ...

Определение потребности работников отделения, распределение их по профессиям и разрядам
Численность рабочих определяется по явочному и списочному составу. Явочный состав основных производственных рабочих определяем по величине производственной программы ремонта вагонов, затрат труда, трудоемкости, нормо-часов, номинального фонда рабочего времени за расчетный период. Явочную потребност ...

Расчет производственной программы предприятия
Производственную программу по эксплуатации АТП рассчитывают, исходя из его производственной мощности и производительности, и выражают в эксплуатационных измерителях. Расчеты ведут по каждой модели автомобилей в отдельности, а затем суммируют по всему парку. Производственная мощность автопарка опред ...